All-cause deaths by date of occurrence, age and sex, England, 2014 - 2022
Methodology
In a couple of weeks, I’m going to write the third and final piece of this series of mortality analyses on England:
I have to wait a couple of weeks for the ONS to prepare and publish the data according to my special request1.
I was going to include a detailed section on methodology in the analysis but it would be at the end of what is already likely to be a lengthy piece, so I thought I would give it its own article here instead and refer to it.
Previously, I only requested data broken down by age. You can see the raw data here: Daily deaths by date of occurrence, 1st June 2014 to 31st May 2022 by single year of age, England.
The methodology will be the same, even though the data stratification may be different.
Firstly, I aggregate the data by age groups, rather than single year, otherwise there will be too many datasets to work with and some will not have sufficient data to do meaningful analysis.
In this example (and probably the final analysis too) I lump together all deaths over 75 years old. The mortality distributions for all those ages are very similar, as are the vaccination rates (which will inevitably form a significant part of the analysis, going where the Expert™ analysts dare not tread for fear of losing their blood money).
Below 75, I group deaths in 5-year ranges that match the vaccination data provided by the UK Coronavirus Dashboard, which incredibly, is still publishing such valuable data despite people like me “misinterpreting” it (for no apparent reason apart from our own ignorance?!).
Next, I plot the raw data to check for any obvious errors and to get an overall sense of what is going on.
It looks like the data is clean. The spikes of COVID epidemic (spring 2020) and COVID “vaccination” drive (winter 2021) are evident. There appears to be no significant underlying general trend. Deaths appear to be back to normal from summer 2021 onwards. Hoorah! COVID, the disease that disproportionately affects old, sick people, is over!
There is a sharp drop off at the end of the series. This is due to reporting delays and can be controlled for.
By simply adding a 3-order polynomial fit to an end section of the 2021-2022 cumulative plot (black dotted line above), we can estimate that there are around 5,000 deaths not yet reported2.
And, already we can see that COVID hit this age group towards the end of a mediocre mortality season in 2019-2020 (red line) but deaths have been higher than expected since early autumn in the following season (green line), probably due to the COVID interventions of spring/summer, before shooting higher in the same rate as the original epidemic when the mRNA experiment begins in the winter.
By the by, I’m still waiting (since 26th June 2022) for the Coroner’s Office to confess how many enquiries they are making into the deaths of young people since the “vaccine” rollout, compared to prior periods3. Don’t hold your breath!
Looking at pretty charts of raw data can be instantly insightful but a little bit of modelling can help substantially. I don’t mean the kind of garbage theoretical models farted out by the Experts™ that bear as little semblance to reality as Liz Cheyney’s run for POTUS ‘24! I mean empirical models that help you make sense of real-world data.
One such model is the Gompertz function. I expect most people are somewhat familiar with the Bell Curve, the Gaussian distribution, more commonly referred to as the “normal” distribution? It is very frequently used to show a range of data and the probability of pulling one of those data points at random from the distribution.
It is good for modelling human data, like heights and weights, and so forth, where the majority of people sit in the middle of the distribution with the data falling away on both sides quite uniformly. Some have used this to model patterns of death.
However, there are slight variations on this distribution that have “better fit” to certain empirical datasets like deaths over time for a particular event, such as what we are looking at here.
What I observe, after first being steered in this direction by Prof. Michael Levitt, is that the distribution of deaths is not “normal” but rather it is skewed to the right. This somewhat counterintuitive term actually means that the bulk of the data sits left of centre with a longer, thinner tail to the right.
This is what we have observed countless times with COVID mortality distributions. Intuitively, if you expose a group of people to a somewhat fatal pathogen at the same time, they do not all die at the same time. The weaker ones die first (and quickly) and others die at ever decreasing rates thereafter.
A very appropriate right-skewed distribution for modelling this empirical data is the Gompertz4 function. It has the added advantage of having another really interesting feature - it has a single initial growth rate and decay rate on that growth rate for its entire distribution.
What does this mean in plain-speak and why is it so important? It means that all the data under a perfect Gompertz function must be internally consistent and unaffected by any external influence. In other words, we can use this empirical model to determine if any COVID measures were effective in “flattening the curve” or Safe and Effective™ at reducing death, because this would manifest as reported data sitting below the Gompertz model, derived from the data reported before the intervention is alleged to become effective.
I have derived my own Gompertz function by observation of numerous mortality data sets in midst 2020. It only works on “excess” deaths (inevitably because otherwise there is no “event” to model) so the next step before applying it is to generate that data.
One thing I have certainly learned over the last couple of years is that there are many, many ways to estimate excess death. The methods employed by the official bean counters have revealed themselves to be inadequate. For example, the difference between current data and the 5-year average (which was almost ubiquitous before more inquisitive minds took the baton), tells us nothing about the dynamics of the mortal population.
Some excess deaths models can go too far in my opinion, relying on age-standardised mortality rate trends and changes in population sizes over time. In the spirit of parsimony, introducing too many variables, especially ones notoriously difficult to estimate in themselves, like population size, can yield inferior results.
My preferred method, drawn upon my broad experience in analysing time-series data in capital markets, relies simply on forecasting future “expected” data after linear or polynomial regression. The premise is based on the efficient markets hypothesis5, i.e. that all the information we need about the dynamics of the deaths process is already contained within it.
Here’s the raw data chart again with a linear regression through the average daily deaths of the 3-month summer period for years 2014 to 2019, extended to “predict” the baseline data for 2020 to 2022, i.e. if COVID and COVID policy interventions hadn’t happened.
You see, I made a mistake with my first observation. There is a trend in the data. Baseline deaths in the over 75s is rising by 0.0095 deaths every day. We should make an allowance for that in our analysis. Some models are good!
Now, what I have estimated here is not the excess death, over and above what is expected for the season but over and above baseline, determined by the summer months. This is because I want to compare COVID deaths and subsequent COVID-era deaths to prior seasonal variations.
We can still deduce whether these COVID deaths were “excess” seasonally-adjusted deaths simply by comparing the entire distribution to prior distributions. This has the added advantage of overcoming any issues with the timing of deaths in any given year which we understand are influenced by the climate (not climate change, ha ha!).
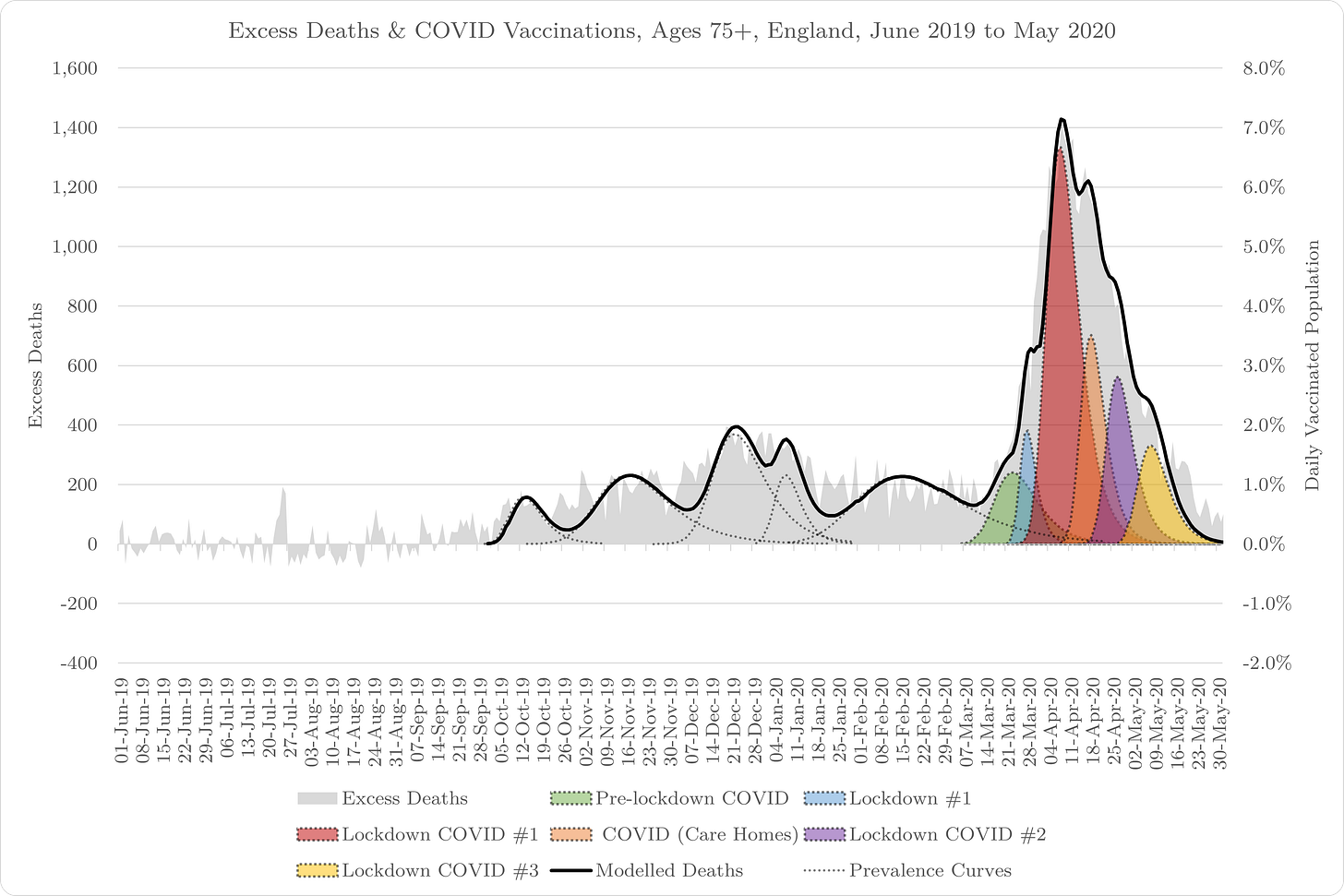
Finally, we can build our Gompertz distributions on the “excess deaths” data.
Above, I have modelled the whole period between June 2019 and May 2020. I run the data between these two mid-year points so that an excess mortality distribution does not span more than one period, making it more difficult to analyse.
As I said, my Gompertz function has only two parameters - a starting growth rate (r) and a decay rate (d). By eye, I pick the point at the start of a new distribution, 6th Oct 2019, in this case.
Subsequently, I include data up to a point that it does not look like a new distribution is emerging within it. In the case of England, this could be because different regions experience seasonal mortality at slightly different times. The climate doesn’t care so much about geographical boundaries (set by kings, queens and politicians) so much as longitude and latitude after all, no matter how the arrogance of Man thinks they can otherwise control it!
Inevitably, it can also result from new pathogens (or some other fatal event) or new changes to the vulnerability of the host population. <=== LOOK!!!! This last point is possibly going to be very important when we come to look at things like experimental containment policies and medical interventions.
So, having derived the first distribution (the entire distribution given that it is a continuous function, regardless of how little data may have been included in the derivation), we can then take the residual data, i.e. that which does not appear to belong to the model (and therefore the mortality distribution), and start again, and so on and so forth. We call this “boot-strapping” in the markets6.
In passing, a quick note on the derivation process. I sum up the squared residuals (the errors, or “chi-square”) and minimise them by numerically solving for the two parameters. I have a brute of a PC (72 logical processors and 256GB of RAM running 64-bit Excel’s solver function). It takes up to 15 seconds to solve for one distribution which is just enough time for me to multitask, like writing another sentence or two in this article, or à la John Dee, putting the kettle on!
My Gompertz function is rt * e ^ (-t * d), where r is the rate for time t, e is Euler’s Number7, and d is decay. Subsequently, I apply this function to the tally of deaths starting at time zero. This produces a cumulative deaths curve. I break the cumulative down to periodic deaths (daily in this case) so that I preserve the structure of the deaths distribution as well as the overall cumulative total.
Well that was a lot longer than I expected it to be so it’s a good thing I didn’t just append it to the analysis. But, I think it is really important to be transparent in methodology if my analyses are to be considered credible.
As such, I also welcome feedback on it and hope you look forward to seeing the final analysis as much as I look forward to writing it! It will include the vax data where we can examine any temporal correlations and compare the data before and after the serial jabbing.
UPDATE
ONS have just released the new set of data. Here again is the cumulative seasonal excess mortality for the over 75s to 31st May 22.
41,372 deaths compared to my estimate of 41,283 (see above). Well, that’s not too shabby, is it?! A model is no good, even an empirical one, if you don’t validate it against reality. Anyone got a number for Professor Pantsdown?
Sure enough, I had to shell out an additional £540 to get what should be routinely made available to the public but thankfully, my paid subscribers have already more than covered the cost.
Nevertheless, in my opinion, there is absolutely no excuse for these reporting delays. With the technology that is available today, it is trivial to create a system that allows for virtually real-time reporting of deaths, including useful demographic data. But, I’ll leave that for another post!
I boot-strapped my first interest rate derivatives curve in 1992.







I thought when I grew up I would find out that people who can do this with numbers are not smarter than the rest of us.....
I am 66, and and even if I live to be 100, I KNOW that people who can do this ARE INDEED SMARTER THAN THE REST OF US.
Joel Smalley, I stand in AWE.
Excellent article! Absolutely no idea what any of it meant.
(I was so bad at maths I got thrown out the O Level class and had to do basic arithmetic - not brilliant at that either)
Anyway, I look forward to the main article but don't forget to add Explanations for Idiots to it!