Gompertz Modelling of Excess Mortality - a Corollary

Analysis of England & Wales with a larger dataset. The results may surprise you.

Introduction

I recently discovered a new mortality dataset for England & Wales:

In spite of the obvious pitfall of being registration-date data, since it goes back as far as 1963, and is stratified by sex, it was still useful for further validating my model, referenced below. In particular, it meant I didn’t have to construct a full curve from 5-year integrals of different birth cohorts. Instead, it was possible to derive reliable full distributions from a single birth cohort.

Unfortunately, in “wisdom” only known to public agencies, the dataset has not been updated since Jan 2022, which itself, only included data up to 2020. So, it’s not going to be much use for excess mortality analysis for the current epoch.

You can read about the main features of the original model and how I got to it here:

---

Analysis

There were 280 mortality distributions that had to be modelled individually - birth years 1880 to 2020 for men and women but to be concise, I am only presenting the results of the women.

It was apparent that there were at least four different distributions (regimes) based on age at death (Figure 1):

1. Under 1 (not shown);

2. 1 to 13;

3. 14 to 34;

4. 35+.

Because the data only started in 1963, calibrating for the younger age distributions was the most challenging. For example, data for 14 year olds at death was only available for those born after 1977 and that age cohort only ran up to 42 years old at death (since I ignored 2020 for calibration purposes since it was an obvious outlier).

Figure 1

Even then, there was a fair amount of erratic, short-term convexity in these short datasets, which may have been the result of using registration-date data as much as anything genuine in the underlying data.

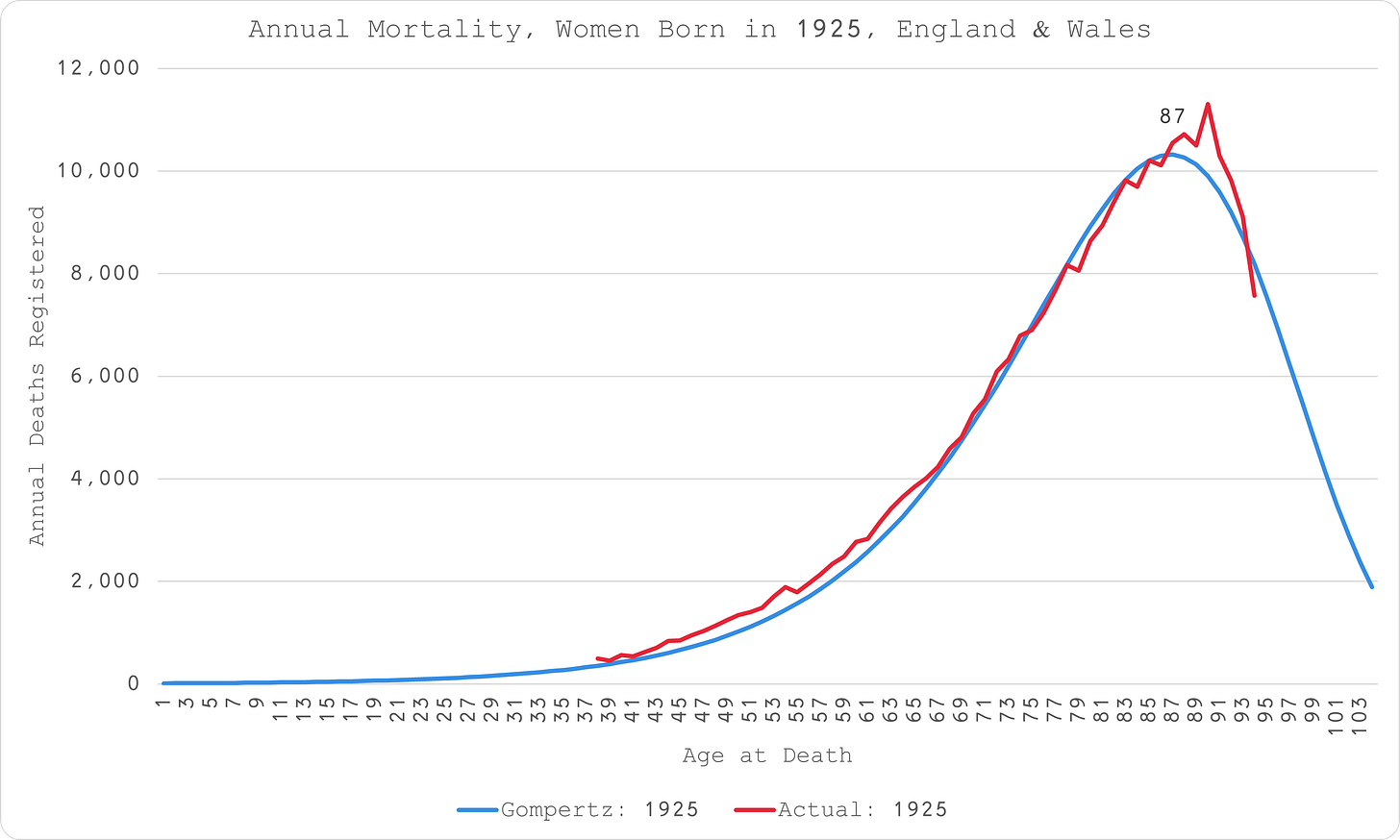
For the older cohorts, there was plenty of data, including over the turn of the Gompertz hump, ably demonstrating the accuracy and robustness of the model - Figure 2.

Figure 2

It is worth noting in Figure 2 that the model does not perfectly fit both ends. This is inevitable as the function is continuous and in this case spans a period of over half a century. For the model to fit both ends would indicate that there has been no improvement in mortality outcomes for that cohort over time.

In addition, there are some obvious outliers that will distort the overall fit since all available data was included in the calibration process. Age at death 87 and 88, for example, are well outside the distribution. Something in years 2002 and 2003 occurred to cause excess mortality so, ordinarily, I would omit these data points when recalibrating in order to get closer to the “normal” or “expected” distribution that would be useful for estimating excess mortality.

2008 was also an outlier, and from other birth cohorts, I could also determine that the whole period 2012 to 2019 was an outlier, seven years of excess, followed by one year (2019) of deficit - Figure 3.

Figure 3

Since most current models for excess mortality only include data going back a max of 10 years, regardless of attempts to capture the dynamics for that period, I am now of the conclusion that they are all unreliable simply by dint of the fact that the baseline data was itself already atypical.

Here is birth cohort 1925 recalibrated up to age 86, i.e. year 2011, instead of 94 (2019) - Figure 4:

Figure 4

Now see how perfectly the single, continuous, two-parameter model fits the entire distribution once the outliers have been omitted from the calibration process. Oh?! Does that mean there has been no public health intervention since 1963 that has improved the mortality expectations of this cohort?

Moreover, it now seems that things actually started going negatively awry in 2010, not 2012. Perhaps we should be looking for public health interventions that resulted in old people dying more rather than less since that time?

---

Results

Plotting the full mortality distributions (derived using the Gompertz model¹) for each birth cohort between 1880 and 1960, every ten years, we can see steady progress in mortality expectations (Figure 5).

Figure 5

As time passes by, the distributions become flatter and more left skewed (longer left tail). In other words, people are living longer and more people are dying later (that isn’t a tautology!²).

Of course, we should expect this. Generally, things like improved nutrition, sanitation, healthcare, etc. should result in exactly this. This also reinforces the premise that birth-year derivations are superior to age-at-death derivations. It’s not just a question of cohort size differences but fundamentally different populations. A 70-year old in 2010 (born in 1940) has a different mortality expectation from one in 2020 (born in 1950), ceteris paribus.

However, since 1960, it looks like things are regressing:

Figure 6

On the face of it, it looks like mortality outcomes for those born in 1970 are not much better than for those born in 1940 and for those born in 1980 are between 1910 and 1930.

Taking the mode of the distributions as a measure of life expectancy (which is more intuitive for me than the arithmetic mean), the picture is clearer (Figure 7):

Figure 7

The progress up to birth cohort 1960 is linear with a notable blip in 1920, immediately following World War I when there was a massive increase in births at a time when I expect resources were still lacking.

Thereafter, it looks like expectations are falling at the same rate that they went up?

However, we should not jump to any immediate conclusions. After in-depth discussion with my peers, it was suggested that the extra convexity in the younger ages that drives the shape of the distribution might be the result of immigration, which has increased substantially since 1960 (Figure 8).

Figure 8

Each year there could be more deaths for all ages simply because the denominator is increasing each year, giving the illusion of convexity that wouldn’t be apparent if this could be compensated for.

Of course, the anomalies in the short-term data, including artefacts of registration delays and perhaps the same adverse events that affected the older age groups between 2012 and 2018 may also be apparent in the younger groups. If that were the case, it would be manifest in the 1970 and 1980 cohorts more than the 1960 ones, since the empirical data for those cohorts is dominated by the atypical period.

---

Conclusion

The longer dataset has helped to validate the propositions made in the original publication. Although it has not been useful in estimating excess mortality for 2020 to 2023, it has informed exactly what data is necessary.

I have asked the ONS to quote for the production of monthly mortality data for those born in England & Wales, stratified by month/year of birth and sex, and by date of occurrence, since 1900. I expect this valuable dataset will be expensive so if anyone thinks this analysis is useful and would like to sponsor it, please let me know!

With this data, we should be able to make more reliable distributions for all cohorts, by finding the inflection points at which the continuity breaks (regime changes), anomalies by year that should be omitted from the model calibrations, resolve the potential immigration confounding, and will not be constrained to full calendar years of deaths (also allowing us to establish seasonal patterns).

I have a very illustrious, multi-disciplined list of potential collaborators (including a pathologist, a biologist, a doctor, a lawyer, a health technologist, a sociologist and various other mathematical scientists) who would be interested in analysing the results which should be quite revealing on many levels, not just in determining the most reliable excess mortality estimates for 2020 to 2023.

We will be able to determine if an event of a particular year (or years) had am impact on some or all birth cohorts; or we could determine if some event affected some or all cohorts when they turned a particular age, e.g. flu jab availability for 65 year olds - things that really should have been routinely monitored by the public agencies for decades?

---

Erratum

I should have clicked on the link in the ONS publication. They most recent dataset was, indeed, updated and released as part of a combined set here:

Still appears to be overdue for 2022 data though.

1. All actual data was included in the calibration in spite of the apparent anomalies since 2012.

2. It is possible for the distribution to be squeezed from both sides, resulting in the same life expectancy but with more people dying at that point. Instead, we have a higher life expectancy and more people dying after that point. This is actually a big problem for health and social care infrastructures if they do not expand and adapt for this extra demand.